Heda (Hermanamientos Escolares Desde las Aulas) es
una red de profesoras y profesores interesados en incorporar las TIC como medio didáctico, ofreciendo no solo un lugar de encuentro, sino también un conjunto de servicios que permita al profesorado explorar, innovar e investigar nuevos enfoques metodológicos con nuevas herramientas didácticas, como los trabajos de colaboración, tanto entre profesores como entre alumnos, la utilización de servicios sociales de la denominada web 2.0, la participación en proyectos nacionales e internacionales utilizando las TIC, la divulgación de la participación en jornadas y congresos en torno a estos temas, recogiendo todas las iniciativas que favorezcan la innovación e investigación en las aulas.

El blog de HEDA es uno de los medios TIC que permite a los participantes del proyecto COMPARTIR la información generada en el proceso de utilización de las TIC en las aulas. Una de las categorías del blog se denomina Buenas PrácTICas 2.0 y dentro de esta categoría han dedicado un artículo al Proyecto Integrado de Joaquín Mesa:
Se plantearon tres tareas o proyectos, uno por cada trimestre, a desarrollar por los alumnos y alumnas de 4º ESO del IES Gran Capitán de Córdoba.
En la primera parte de la primera evaluación los alumnos practicaron la escritura digital, pero como una simple herramienta, esto es, se dieron de alta en el blog de clase y ensayaron la inserción de imágenes, un vídeo, una presentación de Slideshare, un fichero de audio, una presentación de diapositivas con Picasa y, finalmente, combinaron imágenes y audio en una presentación con Slide- el ejercicio que más les divirtió- en diferentes entradas de su blog. Para realizar estos ejercicios les escribí breves tutoriales que les guiaran en estas tareas.
También han dedicado otro artículo a Sisblog:
José Ramón Albendín y Rafael del Castillo son profesores del IES Gran Capitan de Córdoba, su dedicación y acierto en la realización de este blog, donde se dan a conocer trabajos y proyectos realizados por alumnos y sirve de escaparate para las empresas interesadas en colaborar en la Formación en Centros de Trabajo, ha llenado un vacío en los recursos de esta Familia Profesional.
Los miembros del Equipo TIC quieren indicar que se sienten agradecidos y les honra que a los responsables de HEDA les haya gustado la experiencia TIC del centro durante estos últimos cursos.
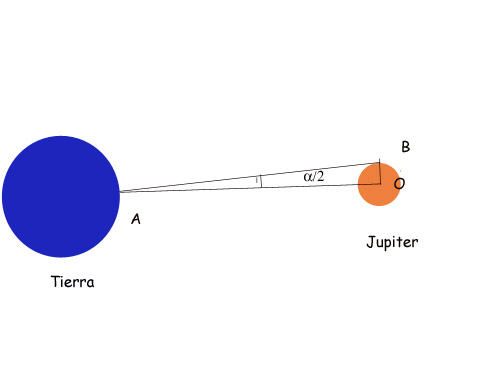




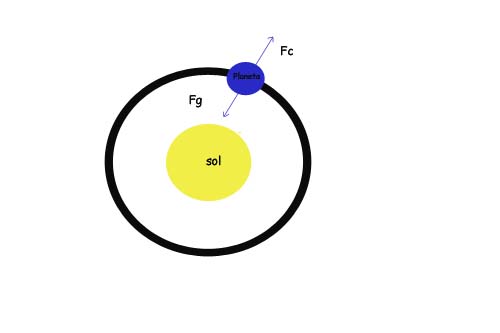
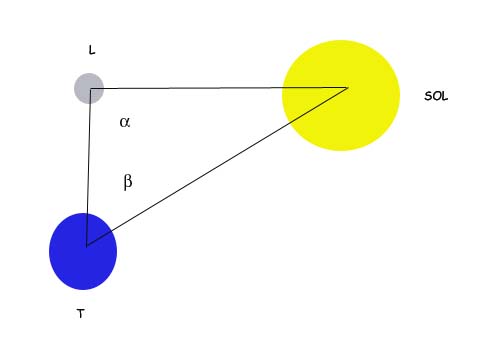

 En el triángulo OAB de la figura, y en el momento de la culminación del Sol, podemos intentar medir los ángulos α y β. Para α no debe haber problema alguno, pues se trata del ángulo que medimos con el gnomon para el problema del radio de la Tierra, y para β, bastaría con utilizar una plomada y un semicirculo por ejemplo. Si apuntamos con un semicirculo invertido en el que previamente hemos colocado una plomada, al centro del Sol y anotamos la medida que marca la cuerda de la plomada en la graduación del semicírculo, estamos midiendo en teoría el ángulo β. Medidos α y β, y conocido el radio de la Tierra, tampoco debe haber dificultad en resolver el triángulo y calcular la distancia de la Tierra al Sol.
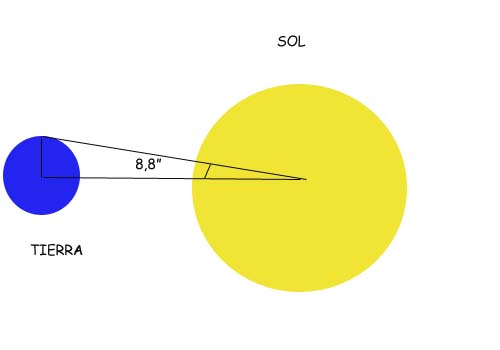
En el triángulo OAB de la figura, y en el momento de la culminación del Sol, podemos intentar medir los ángulos α y β. Para α no debe haber problema alguno, pues se trata del ángulo que medimos con el gnomon para el problema del radio de la Tierra, y para β, bastaría con utilizar una plomada y un semicirculo por ejemplo. Si apuntamos con un semicirculo invertido en el que previamente hemos colocado una plomada, al centro del Sol y anotamos la medida que marca la cuerda de la plomada en la graduación del semicírculo, estamos midiendo en teoría el ángulo β. Medidos α y β, y conocido el radio de la Tierra, tampoco debe haber dificultad en resolver el triángulo y calcular la distancia de la Tierra al Sol.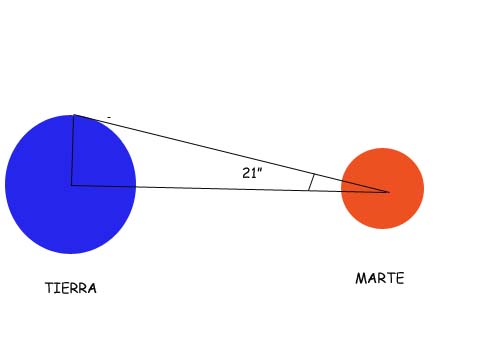


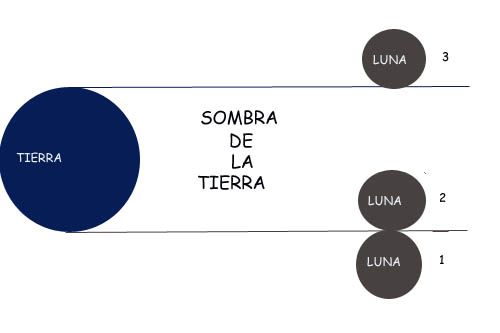
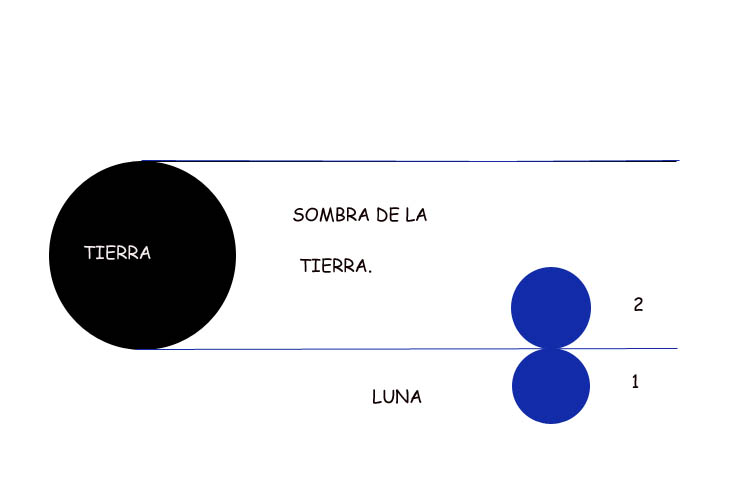 Midió con esto, sin duda, el tiempo que tardó en desplazarse un diámetro lunar completo sobre el fondo del cielo. Lo estimó al parecer en 1 hora.
Midió con esto, sin duda, el tiempo que tardó en desplazarse un diámetro lunar completo sobre el fondo del cielo. Lo estimó al parecer en 1 hora.