CONCURSO DE ASTRONOMÍA. QUINTO PROBLEMA.
ABRIL 2.009.
CÁLCULO DEL PERIODO DE ROTACIÓN DE ALGUNOS PLANETAS.
Basta observar durante un buen rato al telescopio algún planeta del que podamos distinguir algún detalle, para darnos cuenta de que lentamente, muy poco a poco su superficie sufre una rotación.
Para determinar tal rotación, básicamente, bastaría con hacer un seguimiento de algún detalle distinguible sobre la superficie del planeta, tratando de determinar a que velocidad se desplaza sobre su paralelo correspondiente.
En principio, este seguimiento lo podemos hacer de dos maneras:
– Visualmente, con un ocular micrométrico y algún aparato que nos mida el tiempo con precisión, por ejemplo un cronómetro.
Un método que aunque en teoría debe funcionar bien, en la práctica y dependiendo del planeta al que le hagamos el seguimiento puede darnos bastantes problemas.
– Sobre fotografias, hechas con el mismo telescopio y con un intervalo de tiempo lo suficientemente grande como para notar desplazamiento en la superficie y no tan grande como para que el detalle superficial que seguimos pase a la cara oculta para nosotros.
En los casos que nosotros vamos a estudiar, Marte y Jupiter, dos fotografias tomadas con un intervalo entre una y dos horas puede valer.
Esta forma de tomar los datos es más efectiva que la visual.
Vamos a seguir nosotros la rotación de los planetas Marte y Jupiter a través de las excelentes fotografias de dos magníficos astrofotógrafos cordobeses: Jesús R. Sánchez que amablemente nos ha cedido las tomas de Marte, y Manolo Barco que con la misma generosidad nos ha cedido las de Jupiter.

No quiero seguir, sin mostrarles a ambos mi agradecimiento y gratitud por cedernos estas estupendas imágenes.

Voy a intentar ahora ilustraros el proceso a seguir para la determinación de la rotación.
Fijemonos en un detalle sobre la superficie del planeta que sea fácilmente distinguible en las dos fotografias y determinemos el paralelo por el que transita.
Vamos a tomar este paralelo y lo vamos a representar en el plano.
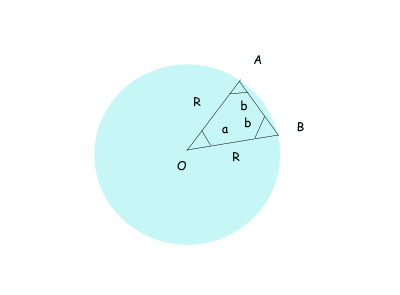
Notemos por O al centro de la circunferencia que forma nuestro paralelo, por A al punto donde se encuentra el detalle a seguir en el instante "t" y por B al punto donde se encuentra en el instante "s". Si nos fijamos en el triángulo AOB, nos encontramos con un triángulo isósceles ( OA y OB son radios del paralelo), del que podemos calcular las medidas de los lados OA, OB y AB ( realmente no medimos el segmento AB sino el arco de la circunferencia entre los puntos A y B, pero esta aproximación supone un error aceptable en nuestros cálculos).
Si notamos por "a" al ángulo con vértice en O y por "b" a los ángulos en los vértices A y B, tendremos:
a + 2b= 180.
Un sencillo cálculo nos permite expresar "b" en función de "a", b = (180-a)/2.
El teorema de los senos nos permite ahora calcular el valor de "a", de la siguiente manera:
AB/sen(a) = OA/sen((180-a)/2); AB sen(90-a/2) = OA sen(a);
entonces: AB (sen(90) cos (a/2) – cos(90) sen(a/2)) = OA sen (a).
luego: AB cos(a/2) = OA sen(2 (a/2)); i.e. : AB cos(a/2) = 2 OA sen(a/2) cos(a/2).
Como tenemos certeza de que 0 < a < 180, pues el detalle a seguir siempre permanece en la misma cara del planeta, podemos deducir que: 0 < a/2 < 90, i.e. : cos( a/2) > 0, y por tanto:
AB = 2 OA sen (a/2).
De donde deducimos por último que AB/2 OA = sen (a/2); o lo que es equivalente, y lo que más nos interesa a nosotros: a/2 = arc sen(AB/2 OA).
El ángulo "a" vale en consecuencia: a = 2 arc sen(AB/2 OA).
Conocido el valor del ángulo "a" lo que conocemos en realidad es el ángulo que ha rotado el detalle distinguible a lo largo de su paralelo en el tiempo "s-t". Si pretendemos saber cuanto tardará en recorrer 360º bastará con hacer una regla de tres.
Bien, deciros por último antes de dar un enunciado formal a los problemas, que debeis pasaros por el Departamento de Matemáticas para recoger copias en papel de las fotografias de Marte y Jupiter que hay que utilizar para las mediciones.
Nos resta por último enunciar los problemas para este mes.
Problema 1: Determinar, utilizando las fotografias suministradas y el método descrito, el periodo de rotación de Marte.
Problema 2: Determinar de la misma manera el periodo de rotación de Jupiter.