CONCURSO DE ASTRONOMÍA. CUARTO PROBLEMA.
MARZO 2.009.
ALGUNAS MEDIDAS SOBRE EL SOL.
Sobre 1.619 y diez años despues de haber enunciado sus dos primeras leyes, Johannes Kepler, en su obra: » Harmonices mundi», anunció el descubrimiento de su tercera ley: » La relación entre el cuadrado del periodo de revolución de un planeta en torno al Sol y el cubo del semieje mayor de su órbita, permanece constante para todos los planetas«.
En otras palabras, si llamamos T al tiempo que tarda un planeta en recorrer su órbita y R al semieje mayor de ésta, se cumple que la razón: T²/R³ vale lo mismo para todos los planetas.
Años más tarde, Isaac Newton, con sus tres leyes y la ley de la gravitación universal, corroboró teóricamente que debía ser así a través del siguiente razonamiento:
Para que se conserve la estabilidad de la órbita de un planeta cualquiera alrededor del Sol, debe ocurrir que la fuerza de atracción Fg entre el Sol y el planeta, debe ser igual a la fuerza centrífuga que tiende a hacer que el planeta escape de la órbita Fc.
i.e.: ha de ocurrir que Fg = Fc.
Ahora bien, ocurre, según la ley de gravitación universal: Fg = G (Ms . Mp)/R².
Donde: G = cte de la gravitación universal. Ms = Masa del Sol. Mp = Masa del planeta.
Y por otra parte, la fuerza centrífuga del planeta en su órbita, que por simplicidad supondremos circular:
Fc = Mp. ap = Mp . (4. ∏²/T²). R
Si ocurre que Fg = Fc, podemos deducir: G. (Ms . Mp) / R² = Mp. (4. ∏²/ T²). R.
Y por tanto: T² / R³ = (4. ∏²)/ G. Ms
Esta igualdad, como vemos, tiene en su segundo miembro una cantidad cte., lo que hace que la razón T² / R³ sea fija para cualquier planeta. Y no sólo esto, sino que esta cantidad, suponiendo conocido el valor de la cte. de la gravitación universal G, sólo depende de la masa del Sol, i. e. si logramos determinar el valor de la cte. T² / R³, conoceriamos el valor de la masa del Sol.
Desde el momento en que Kepler enunció su tercera ley, las distancias relativas entre los planetas conocidos, 6 por aquella época, estaban calculadas.
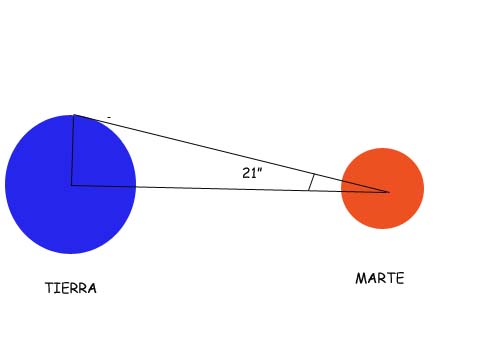
Si notamos por Rt a la distancia entre la Tierra y el Sol, y con algo de paciencia, determinamos el periodo de traslación de algún planeta, pongamos por ejemplo Marte, cuyo periodo real es de 1,882 años terrestres ( 687 dias), podemos escribir, según esta tercera ley:
(1 año)² / (Rt)³ = (1,882 años)² / (Rm)³.
Donde Rm es la distancia entre el Sol y Marte.
Haciendo operaciones, de una manera simple obtenemos que Rm ≈ 1, 52 Rt.
Determinamos así que el radio de la órbita de Marte es aproximadamente 1,52 veces el radio de la órbita de la Tierra.
Y esto sin duda, lo podemos repetir para cualquier planeta, sin más que conocer su periodo orbital.
Como vemos, de esta manera podemos obtener una representación a escala de la medida del sistema Solar, tomando como unidad la distancia que separa a la Tierra del Sol. En adelante, llamaremos a esta distancia unidad astronómica, y la notaremos por U. A.
Si pretendemos tener una idea verdadera de las distancias que nos separan, queda claro, en virtud de todo lo anterior, que necesitamos conocer la distancia real de al menos uno de los planetas al Sol.
Hubo en la antigüedad intentos para calcular esta distancia, de entre ellos cabe destacar el método utilizado por nuestro conocido Aristarco de Samos, quien razonó como sigue:
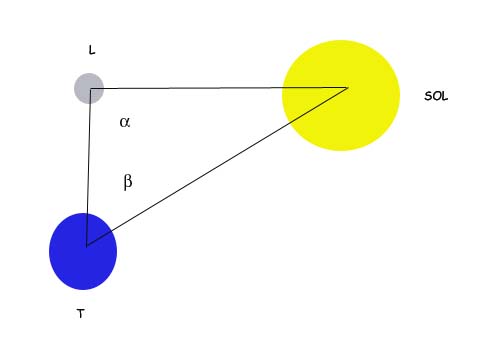
Midió el ángulo β, que forman Luna – Tierra – Sol, cuando la Luna está exactamente en cuarto creciente ( ó en cuarto menguante), momento en que suponía para el ángulo α un valor de 90º.
Medido β, tomando para α un valor de 90º y conocido el valor de la distancia entre la Luna y la Tierra, resolver el triángulo rectángulo no tenía ya dificultad alguna.
Otro método que a nivel teórico puede resultar válido es el descrito a continuación:
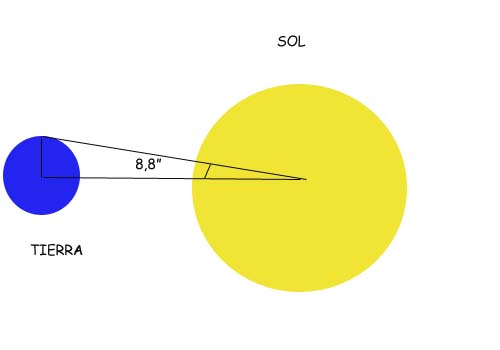
 En el triángulo OAB de la figura, y en el momento de la culminación del Sol, podemos intentar medir los ángulos α y β. Para α no debe haber problema alguno, pues se trata del ángulo que medimos con el gnomon para el problema del radio de la Tierra, y para β, bastaría con utilizar una plomada y un semicirculo por ejemplo. Si apuntamos con un semicirculo invertido en el que previamente hemos colocado una plomada, al centro del Sol y anotamos la medida que marca la cuerda de la plomada en la graduación del semicírculo, estamos midiendo en teoría el ángulo β. Medidos α y β, y conocido el radio de la Tierra, tampoco debe haber dificultad en resolver el triángulo y calcular la distancia de la Tierra al Sol.
En el triángulo OAB de la figura, y en el momento de la culminación del Sol, podemos intentar medir los ángulos α y β. Para α no debe haber problema alguno, pues se trata del ángulo que medimos con el gnomon para el problema del radio de la Tierra, y para β, bastaría con utilizar una plomada y un semicirculo por ejemplo. Si apuntamos con un semicirculo invertido en el que previamente hemos colocado una plomada, al centro del Sol y anotamos la medida que marca la cuerda de la plomada en la graduación del semicírculo, estamos midiendo en teoría el ángulo β. Medidos α y β, y conocido el radio de la Tierra, tampoco debe haber dificultad en resolver el triángulo y calcular la distancia de la Tierra al Sol.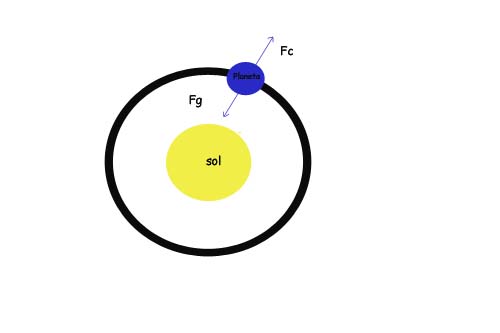

estan muy bien estos problemas felicitaciones
deberian poner mas
Quiero concursar a pesar de que no clasifico, por favor me puede enviar las actividades del concurso para ejercitarme.
Muchas gracias