CONCURSO DE ASTRONOMÍA.
FEBRERO 2.009.
TERCER PROBLEMA.
Entre las mediciones descritas en el problema de Enero, y que efectuó Aristarco, hay una que dá idea del tamaño angular de la Luna en el espacio. Aristarco midió en el eclipse, el tiempo que transcurrió desde que la Luna comenzaba a entrar en el "cilindro" de sombra producida por la Tierra hasta que se ocultó por completo. Midió el tiempo transcurrido entre las posiciones 1 y 2 de la siguiente figura.
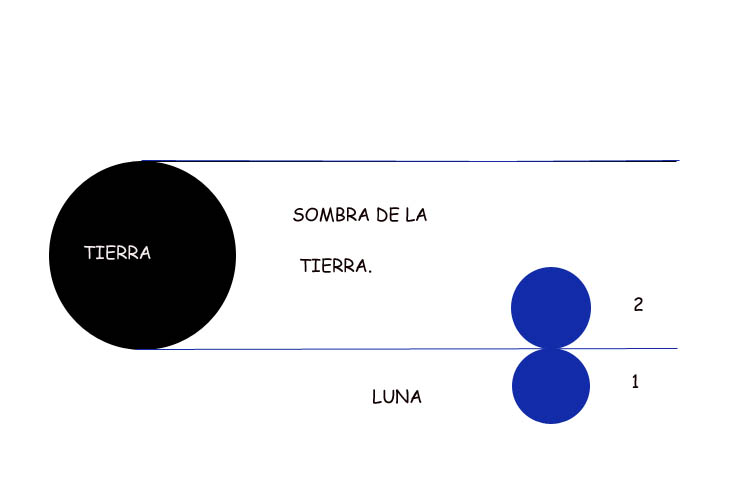Midió con esto, sin duda, el tiempo que tardó en desplazarse un diámetro lunar completo sobre el fondo del cielo. Lo estimó al parecer en 1 hora.
Asignando una medida angular, por ejemplo de xº , a tal desplazamiento ( xº correspondería a 1 diámetro lunar), razonó de la siguiente manera: El periodo de traslación lunar es fácil de determinar y era bien conocido por él, unas 656 horas aproximadamente ( unos 27,3 dias ).
Una simple regla de tres, dá una estimación para "x":
360º_______ 656 horas
xº ________ 1 hora.
Haciendo los cálculos correspondientes obtenemos para "x" un valor de 0,5487º, ó haciendo la conversión a minutos, unos 32,92'.
Si observamos ahora la siguiente gráfica:
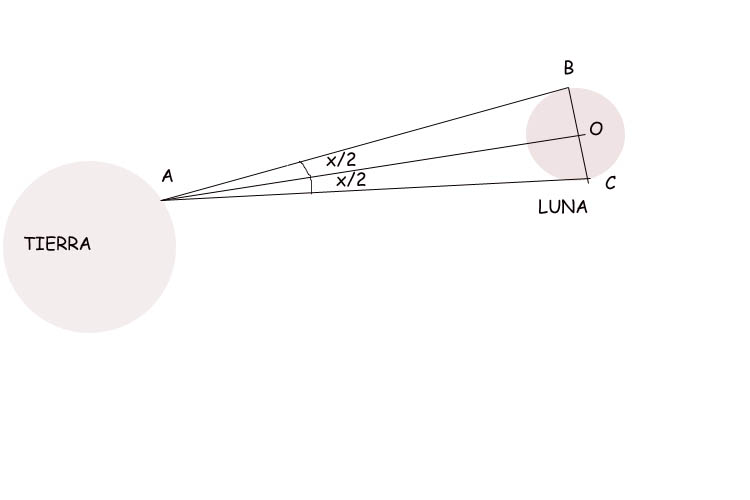
Nos encontramos con un triángulo rectángulo AOB, en el que conocía el ángulo: "x/2" (donde "x" es el ángulo medido anteriormente, por ser el triángulo ABC un triángulo isósceles) y también conocía la medida del lado OB, el radio real de la Luna calculado previamente.
Con estos datos, calcular la longitud del segmento AB era ya un ejercicio trigonométrico muy simple. Conocido en nuestro triángulo rectángulo, la hipotenusa, AB y uno de sus catetos, OB, calcular la longitud del otro cateto, AO no debió ocasionarle muchos problemas. Y es claro que calculando la longitud del segmento AO, estaba calculando la distancia desde su posición, A, hasta el mismo centro de nuestro satélite, O. Hay que insistir, no obstante, en que no se atribuye mucha precisión a los cálculos efectuados por Aristarco.
Parece que fue Hiparco de Nicea (190 a.C.-120 a. C.), al que muchos consideran el primer astrónomo científico, quien mejoró bastante los cálculos efectuados por Aristarco.
Nuevamente, pretender repetir de manera fiel la forma en la que tanto Aristarco como Hiparco tomaron sus mediciones, pasa por esperar un eclipse total de Luna.
Afortunadamente, disponemos de alguna alternativa a esta opción. Para hacer medidas sobre el fondo del cielo con el telescopio, se utilizan unos oculares especiales que llevan impresas unas lineas y unos semicírculos que nos permiten determinar distancias y ángulos. Estos oculares reciben el nombre de oculares "micrométricos", y bien utilizados, junto con una tabla de conversión que contemple las características del telescopio utilizado nos proporcionan medidas bastante fiables.
La próxima Luna llena, la tendremos el dia 9 de Febrero. Os convoco este día, a todos los grupos, o al menos a un miembro de cada grupo, para que obtengais, utilizando los telescopios que tenemos y un ocular micrométrico que yo os proporcionaré, vuestras propias medidas del tamaño angular de la Luna.
Sólo nos queda, creo, dar un enunciado formal para nuestro problema del mes de Febrero:
Problema 1. Calcular la distancia a la que se encuentra la Luna, desde nuestra posición, calculando previamente su tamaño angular.
Nota: Para el radio de la Luna, utilizad todos el mismo valor: 1.738 Km.