CONCURSO DE ASTRONOMÍA.
ENERO 2.009
SEGUNDO PROBLEMA.
Hay que volver a remontarse a la Grecia de los siglos III y II a. C. para buscar los primeros intentos de medición de las dimensiones de Luna, así como la distancia que nos separa de ella.
Paradójicamente, la figura de Aristarco de Samos ( sobre 310 a. C. – sobre 230 a. C.), sea quizás más conocida por unos trabajos que no han llegado hasta nosotros y de los que sólo nos quedan citas de Plutarco y de Arquímedes, que por trabajos suyos que sí han sobrevivido hasta nuestros dias. Los trabajos perdidos, constituyen una defensa del modelo » heliocéntrico», que se oponian a la corriente » geocéntrica» defendida unos años antes por el mismísimo Aristóteles. En el único trabajo que ha llegado a nuestras manos: » De los tamaños y las distancias del Sol y de la Luna» es donde expuso y relató los métodos utilizados para medir las distancias que se citan en el título.
En las fuentes que yo he consultado existen unas mínimas diferencias en la descripción del proceso, vamos a seguir nosotros el método menos sofisticado, en el que se supone (como en el problema del mes de diciembre), que el Sol está lo suficientemente lejos como para que sus rayos nos lleguen paralelos y la sombra producida por la Tierra corresponda a un cilindro y no a un cono.
Bajo esta suposición, se dispuso Aristarco a observar un ecclipse de Luna y tomó las siguientes medidas:
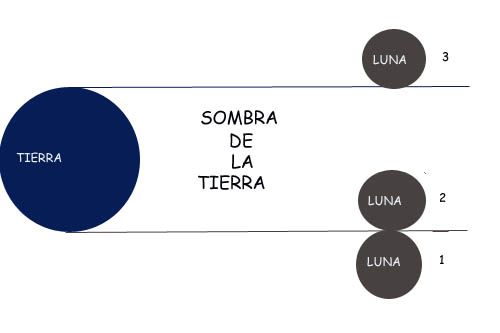
Midió en principio el tiempo que tardó la Luna en pasar de la posición 1 , ( 1ª toma de contacto con la sombra producida por la Tierra) a la posición 2 (momento en que penetra al completo en la sombra).
Midió despues el tiempo que tardó en pasar de la posición 2 a la posición 3.
Suponiendo que el único cuerpo que sufre algún desplazamiento en este tiempo es la Luna, y que se mueve de manera constante, es claro que estas mediciones muestran la relación existente entre los diámetros «d» de la Luna (distancia entre posición 1 y posición 2) y «D» de la Tierra ( distancia entre la posición 2 y la posición 3).
El grado de precisión que obtuvo Aristarco no parece que fuera muy grande, pero la idea y el método han perdurado a lo largo del tiempo, mostrando nuevamente la potencia del razonamiento humano.
Para repetir la experiencia de Aristarco exactamente como él la hizo, tendríamos que esperar al próximo eclipse total de Luna.
Despues de aproximadamente unos 2.300 años, afortunadamente, aunque conservemos la idea ( comparar los diámetros de la Luna y la Tierra), podemos tomar algún «atajo», utilizando la técnica.
Vamos a utilizar algunas fotografias, cedidas cortésmente por el astrónomo aficionado cordobés Paco Bellido (a quien aproveho para mostrar mi agradecimiento), de uno de los últimos eclipses de Luna. Mostramos aquí alguna, pero en papel, podeis recogerlas en el departamente de Matemáticas.


Se trata, de que con los métodos geométricos adecuados ( basicamente, trazar circunferencias que pasan por tres puntos, con regla y compás. Algo que con seguridad habreis hecho alguna vez), delimiteis las dos circunferencias en cuestión, la de la sombra de la Tierra, y la de la Luna. Estudieis la relación existente entre ambos radios, y recordando el valor calculado para el radio de la Tierra, establezcais la regla de 3 correspondiente para calcular el radio de la Luna.
El enunciado de este problema puede quedar así:
Problema 1: Calcular el radio de la Luna, utilizando las fotografías suministradas y conocido el radio de la Tierra. (Utilizad para el radio de la Tierra, la medida oficial de su radio ecuatorial: 6.378 Km.)
Una vez conocido el radio de la Luna, os voy a proponer un problema más:
Paco Bellido, nuestro amable colaborador de este mes, cuenta con algunos «blogs». Entre ellos, en la dirección: www.mizarblogalia.com, en su blog: «El beso en la Luna», aparece un enlace, en su margen derecha, que muestra cartografía lunar de muchos tipos. Clickear en el enlace: «Lunar Map Catalog». Una vez metidos aquí, podeis seguir por ejemplo entrando en » Lunar Landing Site Chart» y abrid aquí la ampliación y resolución que creais más conveniente (si alguno de vosotros prefiere otro tipo de carta en la pantalla anterior, tambien vale). El problema que os propongo, en el que utilizamos tambien unas fotografías suyas, es el siguiente:
Problema 2: Identificar, ayudándose de los mapas de estas páginas, al menos tres cráteres en las fotografías siguientes , y calcular sus dimensiones comparándolas con el radio de la Luna.


Bueno, pues espero que os paseis a recoger las fotos.
Buena suerte a todos. Espero vuestros resultados antes de fin de mes.