CONCURSO DE ASTRONOMÍA. SEXTO PROBLEMA.
Mayo de 2.009.
ALGUNAS MEDIDAS SOBRE JUPITER.
Vamos a finalizar esta serie de problemas intentando conocer algunas medidas de uno de nuestros compañeros en el Sistema Solar: el planeta Jupiter.
Hemos calculado ya en el problema correspondiente al mes de Abril su periodo de rotación.
Su periodo de traslación no es complicado de determinar con algo de paciencia y dedicación y se estima que dura: 11 años, 315 dias y 1,1 horas terrestres.
Con este dato, si recordamos que la razón: T² / R³, donde T= tiempo que tarda un planeta en recorrer su órbita.
y R= el semieje mayor de su órbita, permanece constante para cada planeta. Puesto que conocemos por problemas anteriores los valores de T y R para la Tierra y acabamos de conocer T para Jupiter, podemos deducir el valor de R para Jupiter. Podemos conocer de esta manera la distancia a la que se encuentra Jupiter del Sol. Si pretendemos calcular la distancia que nos separa a nosotros de Jupiter, basta hacer una simple resta:
Si notamos por: R(T) a la distancia entre el Sol y la Tierra
R(J) a la distancia entre el Sol y Jupiter.
Y suponemos las orbitas por simplificación, circulares, tendremos que la distancia entre la Tierra y Jupiter, quedará: d(Tierra, Jupiter)= R(J) – R(T).
Una vez conocdo este dato, si medimos el tamaño angular del planeta con nuestro ocular micrométrico, podemos conocer, utilizando una vez más la trigonometría plana, el radio del planeta.
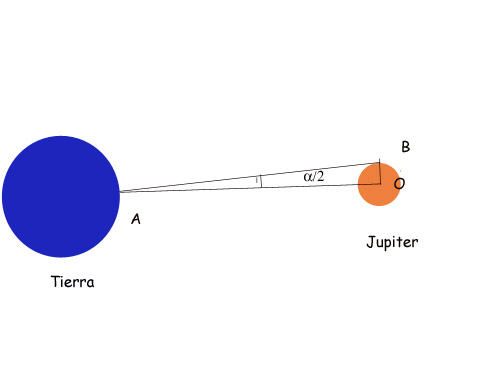
En la imagen anterior, si nos fijamos en el triángulo de vértices AOB, nos encontramos con un triángulo rectángulo (aproximadamente), del que conocemos el ángulo en A ( justo la mitad del tamaño angular del planeta), y el lado OA (conocida la distancia entre la Tierra y Jupiter y el radio de la Tierra, no hay problema en conocerlo). Para determinar el lado OB, basta con proceder de la siguiente forma:
tg (α/2) = OB / OA.
De donde el radio de Jupiter: OB = OA. tg(α/2).
Aunque el tamaño angular del planeta, α, es sin duda algo que podemos medir nosotros, hay que esperar en estas fechas hasta altas horas de la madrugada para poder observar a Jupiter. Es por esta razón por la que tambien vamos a tomar un dato bibliográfico para él. En su última oposición, la de 2.008 rondó su tamaño angular los 48″ de arco, i. e. podemos tomar α = 48″ para nuestros cálculos.
Una vez que conocemos el radio del planeta OB, basta con hacer un seguimiento sistemático del sistema que forma con sus principales satélites ( los satélites Galineanos: Io, Europa, Ganímedes y Calixto, que son facilmente observables con cualquier telescopio), para hacer un cálculo, no sólo de los periodos de traslación de éstos alrededor del planeta, sino para calcular la máxima elongación, i. e. : el radio de las órbitas ( que supondremos por simplificación circulares).
Para hacer este seguimiento es recomendable estar haciendo observaciones al menos durante dos o tres dias, a razón de dos o tres observaciones por noche, y continuar durante 11 ó 12 noches más, con una observación diaria. De esta forma nos aseguramos un seguimiento más o menos bueno para los satélites más rápidos, los más cercanos al planeta, y tambien al prolongarlo durante este tiempo, para los más alejados del planeta y lentos.
Lo más cómodo es hacer este seguimiento tomando fotografías (siempre será más preciso medir distancias sobre papel, que con el ocular micrométrico). Es importante anotar el tiempo con la mayor precisión que podamos.
Os muestro algunas de las que yo tomé este verano para hacer el estudio:
Una vez hechas las observaciones, o tomadas las fotografiás, viene uno de los momentos más delicados: identificar en cada fotografía cada uno de los satélites. Con paciencia y tiempo acabaremos haciendolo pero normalmente hay que dedicarle un buen rato. Una vez identificados, hay que medir cuidadosamente para cada uno de ellos, su distancia a Jupiter, y sí está al Oeste o al Este del planeta. Toda esta información hay que pasarla, una vez que la tengamos a una gráfica, para entender el comportamiento.
Para cada uno de los satélites se toma un folio de papel milimetrado, se toma un sistema de referencia. El eje de abcisas lo dejaremos para el tiempo y el eje de ordenadas para las distancias al planeta, conviniendo por ejemplo que si el satélite se encuentra al Este entenderemos que su ordenada es positiva y que si se encuentra al Oeste su ordenada es negativa.
Hecho esto, nos quedará para cada satélite una gráfica con aspecto sinusoidal en la que podremos ver claramente los datos que buscamos: su máxima separación del planeta, ( el radio de su órbita) y su periodo de traslación.
Si hemos sido cuidadosos en el proceso que os he descrito, obtendremos unas muy buenas aproximaciones a las medidas que se aceptan como reales en la actualidad. Estas medidas, os la muestro en la siguiente tabla:
Satélite Máxima elongación (en radios de Jupiter) Periodo de traslación (en dias)
Io 5,9014 1,769
Europa 9,3910 3,551
Ganímedes 14,9796 7,155
Calixto 26,3579 16,689
Con todos estos datos y bajo la suposición de que las leyes que rigen el movimiento de estos satélites en torno a Jupiter son las mismas que rigen el movimiento de los planetas en torno al Sol, podemos calcular, por 4 veces ahora, la masa de Jupiter, de ma nera análoga a com procedimos para calcular la masa del Sol, i. e.: utilizando:
T² / R³ = (4.Π²) / (G.M).
Donde: G= cte de la gravitación universal.
T= periodo de traslación del satélite.
R= radio de la órbita del satélite.
M= masa de Jupiter.
Conocida la masa del planeta, seguro que se os ocurre calcular algunas otras cosas, pero sabiendo que se avecinan los exámenes no os voy a robar más tiempo con esto.
Vamos a enunciar de esta manera los últimos problemas de nuestro concurso.
Antes de hacerlo, deseo hacer una nota a modo de despedida: Mi experiencia con esto ha sido positiva, me ha gustado ver como crecía en vosotros el interés por investigar mínimamente sobre estos números que suelen ser lo que menos ocupa en los libros y lo más trabajoso de descubrir. Lo que pone el límite de las mejores mentes de cada generación y nos muestra de la manera más expresiva que conocemos lo que representamos en la globalidad del Universo. Espero que a vosotros os haya servido para algo, sólo eso estaba en mi mente cuando decidí iniciarlo.
Deseo que os vaya estupendamente en vuestros estudios uninversitarios.
En fin, paso ya a enunciar los problemas.
Problema 1: Calcular la distancia de la Tierra a Jupiter.
Problema 2: Calcular el radio del planeta Jupiter.
Problema 3: Calcular su masa.
Recordaros por último que sobre finales de mes, se harán públicos los nombres de los equipos ganadores.
Buena suerte a todos. Me ha gustado mucho compartir esto con vosotros.