TICágora

CONCURSO DE ASTRONOMÍA

DICIEMBRE 2008

PRIMER PROBLEMA:

ERATÓSTENES Y EL RADIO DE LA TIERRA. VOLUMEN.

NEWTON Y LA MASA DE LA TIERRA. DENSIDAD.

1. Basta teclear en nuestro ordenador la palabra «Eratóstenes» en algún buscador potente, para que aparezcan del orden de centenares de miles de entradas que la contengan. En muchas de ellas, encontraremos una pequeña biografía de nuestro personaje y una descripción de lo que aportó a la ciencia de la época. La mayoría narran la mayor proeza de nuestro personaje: medir la longitud de un meridiano terrestre sin más instrumentos que un palo y mucha imaginación.

Nació Eratóstenes de Cirene sobre el año 280 a. C., conoció a Arquímedes, y fue llamado sobre el 236 a. C. para que se hiciera cargo de la Biblioteca de Alejandría. La dirigió hasta el fin de sus dias, hecho que tuvo lugar sobre el 194 a. C.

Era conocido por sus contemporáneos bajo el apodo de: «el beta» («β», segunda letra del alfabeto griego) porque parece ser que era el segundo en todo aquello que hacía. En lo que se refiere sin embargo a este logro, superó con creces esa segunda posición.

Parece que fue en la Biblioteca, donde leyó en un papiro, que en la ciudad de Siena ( hoy Asuán, en Egipto), el día del solsticio de Verano, a mediodía, los objetos no proyectaban sombra alguna, y el Sol se reflejaba en el fondo de los pozos. Se aprestó entonces a ver si en Alejandría ocurría igual que en Siena. Y comprobó como los objetos en Alejandría, el dia 21 de junio al mediodía proyectaban sombra. Suponiendo que el Sol lo suficientemente lejos, y es tan grande como para que sus rayos nos lleguen paralelos, la primera conclusión era evidente: la Tierra no podía ser plana. Admitiendo entonces que pudiera tener forma esférica y que Siena y Alejandría pudieran estar ambas en el mismo meridiano, midió la sombra que proyectaba en Alejandría un palo vertical sobre la superficie, y haciendo el gráfico que se ilustra a continuación llegó a la conclusión de que los rayos del Sol que a Siena llegaban en vertical, llegaban a Alejandría con una inclinación de alrededor de 7º.

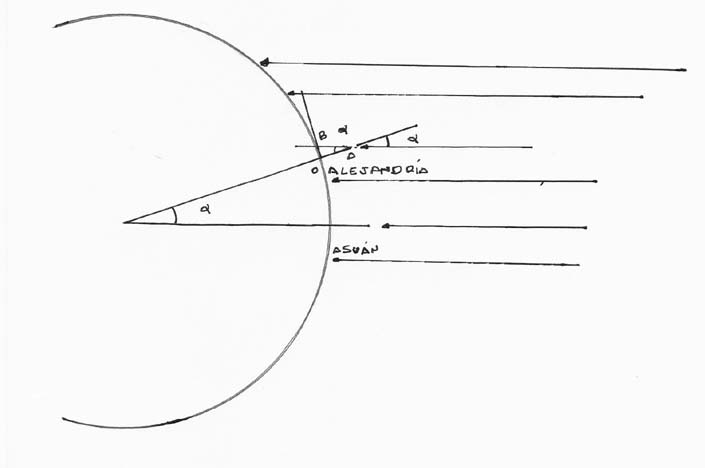
Dado que dicha inclinación α coincide, como vemos, con la porción angular del meridiano en cuestión, se obtiene directamente que la porción de este meridiano entre Siena (Asuán) y Alejandría corresponde exactamente a 7º.

Intentó averiguar, después de medir el ángulo, la distancia real entre ambas ciudades, y la cifró en unos 800 Km. aproximadamente.

Le restaba hacer una simple regla de tres para determinar la medida del meridiano completo.

Con estos datos, podéis comprobar vosotros mismos como la medida del meridiano completo debe ser 41.143 Km.

Para deducir por último el radio de la Tierra, le restaba recordar la relación existente entre la longitud y el radio en una circunferencia.

Para estos números que nosotros manejamos, se comprueba sin dificultad que queda un radio terrestre de aproximadamente 6.548 Km.

La medida que se acepta actualmente para el radio polar de la Tierra es de unos 6.356,75 Km. Como vemos, para la época y para la forma en la que se hizo, el radio obtenido por Eratóstenes es una muy aceptable aproximación de la medida real.

De toda la narración anterior, la pregunta más delicada es sin duda la siguiente: ¿ Cómo midió Eratóstenes el ángulo α ? Para responderla, observemos el triángulo de vértices O,A,B de la figura anterior, algo ampliado:

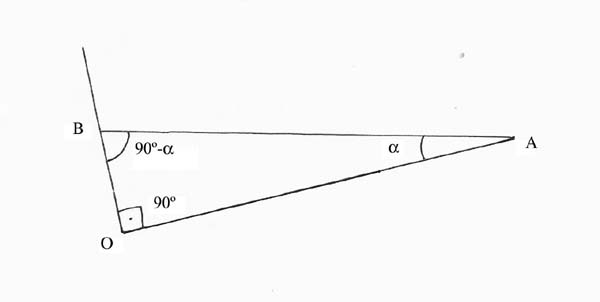
Conocida la longitud del palo vertical OA, la longitud de la sombra que proyecta OB, y el hecho de que la recta tangente OB y la recta normal OA en el punto de tangencia O forman un ángulo de 90º, resulta fácil recordar que se cumple:

tg α = OB/OA.

En la época de Eratóstenes ya se disponía de los conocimientos que se requieren para estos cálculos. Para nosotros con nuestras «potentes» calculadoras, conocer desde aquí el ángulo α, es simplemente cuestión de tomar dos medidas y teclear apropiadamente en nuestros aparatos.

Intentar repetir desde nuestra posición el experimento de Eratóstenes, pasa por buscar un lugar en nuestro mismo meridiano, no demasiado cercano, y medir la inclinación con la que los rayos solares inciden en las dos posiciones seleccionadas, en el mismo momento, y que éste sea el momento de la culminación del Sol.

Profesores del I. E. S. de Llanes, en Asturias, a quienes quiero agradecer el gesto y la colaboración, van a compartir con nosotros la experiencia. Haremos las mediciones, un día de mediados de diciembre, que ya os comunicaremos con antelación.

Pero ocurre que nosotros tenemos un problema añadido que no tuvo Eratóstenes: en ninguna de nuestras posiciones va a incidir el Sol, ningún día del año ni a ninguna hora, sin que los objetos proyecten sombra alguna. Seguro que si pensais un poquito sobre esto, hallareis vosotros mismos la razón.

Para entender ahora nuestra situación real, observemos la siguiente figura:

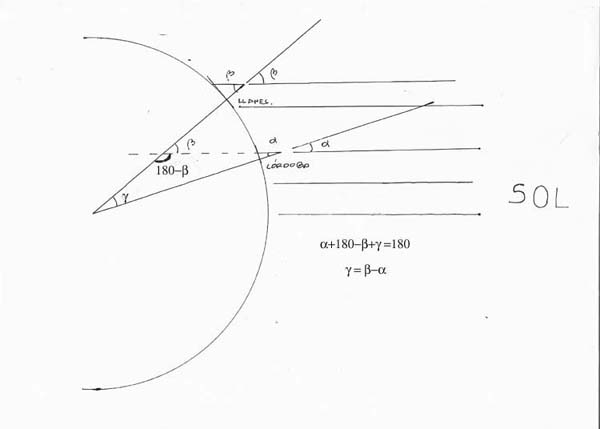
Vemos, como midiendo los ángulos α y β, podemos conocer ahora la porción angular γ, del meridiano que pasa por ambos puntos. La relación existente entre estos tres ángulos es: γ=β-α. Si supieramos la distancia real que separa a Córdoba de Llanes, nos restaría hacer otra regla de tres para calcular la longitud del meridiano correspondiente. Conocida la longitud del meridiano, conocer la del radio polar es ya bastante simple.

Bien, pues el primer problema correspondiente al mes de diciembre queda ya planteado: Calcular la medida del radio polar terrestre, repitiendo la experiencia de Eratóstenes.

Para hacer la medición necesaria, (medir la sombra proyectada por un palo vertical simultáneamente en los lugares seleccionados, en el momento de la culminación del Sol) hay disponibles en el Departamento de Matemáticas unos gnomom, fabricados y facilitados por los profesores y alumnos del Departamento de Madera, a quienes quiero agradecer su colaboración.

2. Como segundo problema para este mes, y conocido el radio de la Tierra, suponiendo para ésta una esfericidad perfecta, no podemos pasar de aquí sin calcular su volumen, para lo que necesitamos una sencilla fórmula matemática. Planteamos pués:

Segundo problema: Cálculo del volumen de la Tierra.

3. Para seguir con el estudio de la Tirra, damos un buen salto en el tiempo, nos vamos al siglo XVII y acudimos ahora a los aportes a la ciencia, de uno de los mayores científicos de todos los tiempos: Isaac Newton, para intentar determinar la masa de nuestro planeta.

Es sin duda Newton, uno de los científicos más conocidos, y su justa y merecida fama es debida a sus estudios tanto en Matemáticas como en Física. En Matemáticas gracias a él y a un matemático algo menos conocido: Leibnitz, disfrutamos de una de los herramientas más potentes y con mayor aplicación a la ciencia:el cálculo diferencial. En Física: ¿quién no conoce las leyes de Newton o la ley de la gravitación universal?. Es justamente ésta última, de la que nos vamos a servir para calcular la masa de la Tierra.

Asegura la ley de la gravitación universal de Newton, que la fuerza F, con la que dos cuerpos se atraen, es directamente proporcional al producto de sus masas M y m, e inversamente proporcional al cuadrado de la distancia entre sus centros de gravedad r.

Matemáticamente: F = G·(M · m / r²)

Donde G es la constante de proporcionalidad llamada constante de proporcionalidad universal.

Antes de seguir, conviene hacer el comentario de que Newton no llegó a conocer el valor de la constante G. Fue años más tarde, cuando el físico Henry Cavendish ideó un dispositivo para determinar su valor, que se fijó en 0,00000000006672 unidades internacionales, i.e. cuando las masas se dan en Kilogramos, la distancia en metros y la fuerza en Newtons.

Después de conocer el valor de la constante de gravitación universal, conocer la masa de la Tierra pasa por utilizar la ley de la gravitación de la siguiente manera:

Tomando un cuerpo cualquiera en la superficie terrestre del que conozcamos su masa «m», si pensamos que la fuerza con que la Tierra y este cuerpo se atraen es el propio peso del cuerpo, y despejamos la masa de la Tierra «M», de nuestra fórmula, obtenemos:

M = (F · r²)/(G · m)

Asumiendo por último que la distancia que separa los centros de gravedad de ambos cuerpos (la Tierra y nuestro objeto ) es el propio radio de la Tierra, ya conocido por nosotros desde el problema 1, en la igualdad anterior, sólo desconocemos la masa de la Tierra «M». Basta para conocerla hacer los cálculos pertinentes.

Queda de esta forma planteado el problema 3 en la forma siguiente:

Problema tercero: Calcular la masa del planeta Tierra.

4. Para finalizar los problemas de este mes, conocidos la masa y el volumen de la Tierra, no podemos desaprovechar la ocasión para calcular la densidad media de nuestro planeta:

Problema cuarto: Calcular la densidad media del planeta Tierra.

En resumen, para este mes, debeis entregar antes de irnos de vacaciones, o como muy tarde el día de la vuelta, i.e. el dia 8 de enero las respuestas a las siguientes preguntas:

Primer problema: Cálculo del radio de la Tierra, repitiendo la experiencia de Eratóstenes.

Segundo problema: Cálculo del volumen de la Tierra.

Tercer problema: Cálculo de la masa de la Tierra.

Cuarto problema: Cálculo de la densidad de la Tierra.

Para el experimento de Eratóstenes, pasad a recoger vuestro gnomon por el Departamento de Matemáticas a partir del día 10. Ya os comunicaremos el día concreto en el que se realizarán las medidas.

Buena suerte a todos y muchas gracias a todas las personas que van a colaborar con nosotros. En especial a los profesores y alumnos del Departamento de Madera de nuestro Instituto, y a los profesores y alumnos implicados en el I.E.S. de Llanes, en Asturias.